Traverse an M * N 2D array in spiral order clock-wise starting from the top left corner. Return the list of traversal sequence.

Assumptions

• The 2D array is not null and has size of M * N where M, N > = 0

Examples

{ {1, 2, 3, 4},

{5, 6, 7, 8},

{9, 10, 11, 12} }

the traversal sequence is [1, 2, 3, 4, 8, 12, 11, 10, 9, 5, 6, 7]

Solution: 注意有3种情况：什么都不剩，剩一行，剩一列

  public List<Integer> spiral(int[][] matrix) {
    List<Integer> ans = new ArrayList<>();
    if (matrix.length == 0 || matrix[0].length == 0) {
      return ans;
    }
    int start = 0, end = matrix[0].length - 1, start2 = 1, end2 = matrix.length - 2;

    //其实应该start2 = 0, end2 = matrix.length - 1,这样更简单：while (start < end && start2 < end2)
    while (start < end && (start2 <= end2 || start2 - end2 == 1)) {
      for (int i = start; i <= end; i++) {
        ans.add(matrix[start][i]);
      }
      for (int i = start2; i <= end2; i++) {
        ans.add(matrix[i][end]);
      }
      for (int i = end; i >= start; i--) {
      //注意不是matrix[end][i]
        ans.add(matrix[end2 + 1][i]);
      }
      for (int i = end2; i >= start2; i--) {
        ans.add(matrix[i][start]);
      }
      start++;
      end--;
      start2++;
      end2--;
    }
    //剩一行
    if (start < end) {
      for (int i = start; i <= end; i++) {
        ans.add(matrix[start][i]);
      }

    }
    //剩一列
    if (start == end) {
      for (int i = start; i <= matrix.length - 1 - start; i++) {
        ans.add(matrix[i][start]);
      }
    }
    return ans;
  }

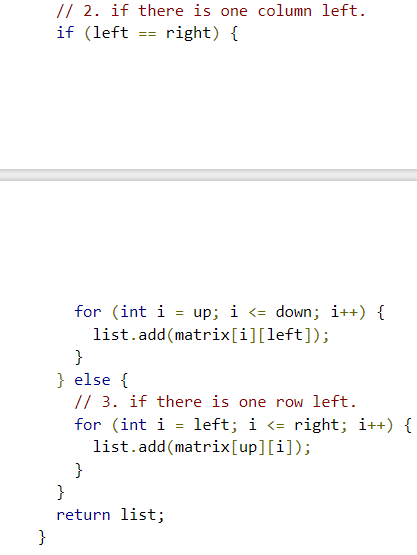
better way: left = 0, right = n - 1, up = 0, down = m - 1